Графы
Графы являются описаниями автоматизаций в системе Атом.Порт. Согласно им выполняются задачи конфигурирования удалённых компьютеров и сохраняется некоторая информация о них.
Документ разъясняет принятый синтаксис сериализации графов версии 2.
1. Введение
💾 Актуально для версии Атом.Порт:
63ef9982
Общие сведения
Язык конфигурации графов Атом.Порт — простой предметно-ориентированный язык на базе языка разметки YAML. Он предназначен для создания автоматизаций произвольной сложности. Язык описывает последовательный и условный вызов функции SaltStack.
В документе используются следующие синонимичные наименования типов:
- Список — sequence (последовательность).
- Словарь, объект — mapping (сопоставление).
Структура автоматизаций
Автоматизация Атом.Порт — это последовательность операций, всегда связанная с одной рабочей станцией. Описание последовательности операций называется графом Атом.Порт. Граф Атом.Порт представляет собой ориентированный взвешенный граф с истоком, называемым начальным узлом start и стоком, называемым конечным узлом end. Граф состоит из узлов (вершин), соединённых взвешенными ориентированными рёбрами (дугами). Вес дуги определяет выбор пути от истока к стоку и обратен по смыслу приоритету, т. е. выбирается путь с наименьшим весом. Таким образом, исполнение автоматизации представляет собой проход по графу от начальной до конечной вершины.
Пример абстрактного орграфа на рисунке. Зелёным обозначен путь от истока к стоку, числами веса рёбер.
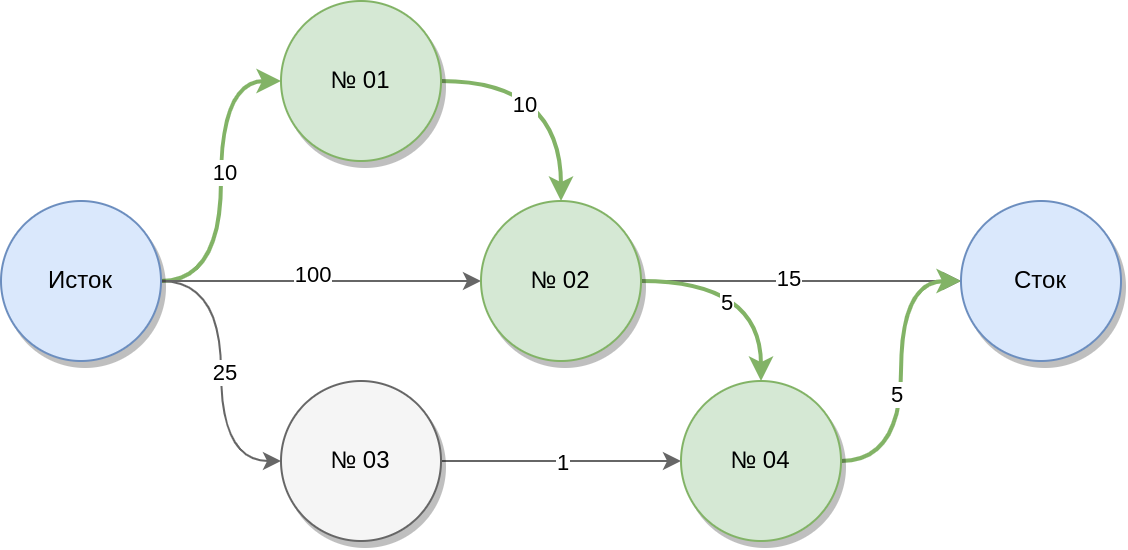
Следствия такой структуры:
- Граф имеет один или более путей от начального узла к конечному.
- Некоторые вершины графа могут быть непосещёнными (т. е. связанные с такими вершинами никогда не будут выполнены) после прохода графа.
- Всегда выбирается путь с наименьшим общим весом. Вес дуи может изменяться в процессе прохода по графу. Так, дуга к узлу, отмеченному успешно пройденным, становится невесомой, т. е. её вес становится равным 0. Вес дуги к узлу, пройденному неуспешно, т. е. в случае неуспешного выполнения операции, становится бесконечным.
- Автоматизация, вес кратчайшего пути которого вырос до бесконечного, считается неуспешным: нет возможности достичь конечной вершины.
- В настоящее время циклы в пути не допускаются.
Операции могут быть как удалёнными действиями, выполняемыми посредствам вызова функций SaltStack, так и активностями сервера. Подробнее о типах операций см. главу об узлах.
Синтаксис
Один граф описывается одним конфигурационным файлом в формате ключ: значение. Сложные значения (списки и словари) задаются в виде блоков, выделямых равными пробельными отступами (в обычно 2 или 4 символа пробела):
список:
- значение_1
- значение_2
словарь:
ключ_1: значение
ключ_2: значениеСписок содержит упорядоченные элементы, которые могут повторяться. Порядок ключей словаря не учитывается, ключи не должны повторяться.
Строчные литералы рекомендуется оборачивать одинарными (') или двойными (") кавычками для однозначности, хотя в большинстве случаев это не обязательно. Числовые и булевы литералы следует указывать без кавычек.
При выгрузке графов система составляет названия файлов из названия графа и суффикса «yaml». Такого же именования следует придерживатьяс при написании файлов графов вручную. В названиях графов желательно использовать латиницу без пробелов, например: install-packages. Файл следует (хотя и не обязательно) начинать со знака начала документа ---, за которым следуют параметры name и description , затем прочие ключевые слова, рассматриваемые далее.
О загрузке и выгрузке файлов графов средствами командного интерфейса можно узнать на странице, посвящённой служебным командам.
ауавававуРоCmxGraphModel%3E%3Croot%3E%3CmxCell%20id%3D%220%22%2F%3E%3CmxCell%20id%3D%221%22%20parent%3D%220%22%2F%3E%3CmxCell%20id%3D%222%22%20value%3D%22%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0%3BentryY%3D0.5%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3BstrokeWidth%3D2%3B%22%20edge%3D%221%22%20source%3D%228%22%20target%3D%2211%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%223%22%20value%3D%2210%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%222%22%3E%3CmxGeometry%20x%3D%220.0512%22%20y%3D%22-2%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%224%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0%3BentryY%3D0.5%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23f5f5f5%3BstrokeColor%3D%23666666%3B%22%20edge%3D%221%22%20source%3D%228%22%20target%3D%2214%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%225%22%20value%3D%2225%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%224%22%3E%3CmxGeometry%20x%3D%220.0128%22%20y%3D%222%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%226%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0%3BentryY%3D0.5%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23f5f5f5%3BstrokeColor%3D%23666666%3B%22%20edge%3D%221%22%20source%3D%228%22%20target%3D%2219%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%227%22%20value%3D%22100%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%226%22%3E%3CmxGeometry%20x%3D%22-0.0597%22%20y%3D%223%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%228%22%20value%3D%22%D0%98%D1%81%D1%82%D0%BE%D0%BA%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%23dae8fc%3BstrokeColor%3D%236c8ebf%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22120%22%20y%3D%22140%22%20width%3D%2280%22%20height%3D%2280%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%229%22%20value%3D%22%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0.5%3BentryY%3D0%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3BstrokeWidth%3D2%3B%22%20edge%3D%221%22%20source%3D%2211%22%20target%3D%2219%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%220.3336%22%20y%3D%22-10%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2210%22%20value%3D%2210%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%229%22%3E%3CmxGeometry%20x%3D%22-0.2988%22%20y%3D%22-12%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2211%22%20value%3D%22%E2%84%96%2001%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22260%22%20y%3D%2240%22%20width%3D%2280%22%20height%3D%2280%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2212%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0%3BentryY%3D0.5%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23f5f5f5%3BstrokeColor%3D%23666666%3B%22%20edge%3D%221%22%20source%3D%2214%22%20target%3D%2222%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2213%22%20value%3D%221%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%2212%22%3E%3CmxGeometry%20x%3D%220.0156%22%20y%3D%22-1%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2214%22%20value%3D%22%E2%84%96%2003%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%23f5f5f5%3BstrokeColor%3D%23666666%3BfontColor%3D%23333333%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22260%22%20y%3D%22230%22%20width%3D%2280%22%20height%3D%2280%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2215%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0%3BentryY%3D0.5%3BentryDx%3D0%3BentryDy%3D0%3Belbow%3Dvertical%3Bcurved%3D1%3BfillColor%3D%23f5f5f5%3BstrokeColor%3D%23666666%3B%22%20edge%3D%221%22%20source%3D%2219%22%20target%3D%2223%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2216%22%20value%3D%2215%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%2215%22%3E%3CmxGeometry%20x%3D%22-0.074%22%20y%3D%221%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2217%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0.5%3BentryY%3D0%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3BstrokeWidth%3D2%3B%22%20edge%3D%221%22%20source%3D%2219%22%20target%3D%2222%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2218%22%20value%3D%225%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%2217%22%3E%3CmxGeometry%20x%3D%22-0.2247%22%20y%3D%22-11%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2219%22%20value%3D%22%E2%84%96%2002%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22360%22%20y%3D%22140%22%20width%3D%2280%22%20height%3D%2280%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2220%22%20style%3D%22edgeStyle%3DorthogonalEdgeStyle%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0%3BentryY%3D0.5%3BentryDx%3D0%3BentryDy%3D0%3Bcurved%3D1%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3BstrokeWidth%3D2%3B%22%20edge%3D%221%22%20source%3D%2222%22%20target%3D%2223%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2221%22%20value%3D%225%22%20style%3D%22edgeLabel%3Bhtml%3D1%3Balign%3Dcenter%3BverticalAlign%3Dmiddle%3Bresizable%3D0%3Bpoints%3D%5B%5D%3B%22%20vertex%3D%221%22%20connectable%3D%220%22%20parent%3D%2220%22%3E%3CmxGeometry%20x%3D%22-0.1568%22%20y%3D%222%22%20relative%3D%221%22%20as%3D%22geometry%22%3E%3CmxPoint%20as%3D%22offset%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2222%22%20value%3D%22%E2%84%96%2004%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%23d5e8d4%3BstrokeColor%3D%2382b366%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22460%22%20y%3D%22230%22%20width%3D%2280%22%20height%3D%2280%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%2223%22%20value%3D%22%D0%A1%D1%82%D0%BE%D0%BA%22%20style%3D%22ellipse%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3Baspect%3Dfixed%3BfillColor%3D%23dae8fc%3BstrokeColor%3D%236c8ebf%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22600%22%20y%3D%22140%22%20width%3D%2280%22%20height%3D%2280%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3C%2Froot%3E%3C%2FmxGraphModel%3Eава